裂區實驗設計﹙split-plot design﹚之實務運用

前言：

　　裂區實驗設計（split-plot design）是由費雪爵士（Sir Ronald Aylmer Fisher）所發明，起初運用於農業實驗，然而許多工業實驗在實務上也是以裂區實驗設計的方式進行，卻被誤認為是完全隨機實驗（completely randomized experiment），因而作了錯誤的資料分析。

　　當工業實驗面臨特定實驗因子水準不易改變或受限於經濟效益之考量（如批量的大小），通常無法進行完全隨機實驗，也就是實驗者必須遷就現實，“刻意”配置實驗因子組合的方式，讓不易改變的實驗因子其改變水準的次數最少化。在這種隨機限制（restriction on randomization）的情況下，就必須以裂區實驗的架構進行實驗，也就要能清楚分辨哪些是屬於全區因子（whole-plot factors），哪些是屬於副區因子（sub-plot factors），如此才能避免不正確的分析結果。

　　近年來雖然有多位統計專家針對裂區實驗發表許多新的應用與解析手法，但在工業實驗方面仍然尚未受到應有的重視與了解，本文就先以簡單且典型的例子（1），也就是實驗配置中包含一個不容易變更水準的實驗因子和一個容易變更水準的實驗因子，來說明裂區實驗的本質以及如何正確的進行裂區實驗變異數分析（ANOVA）。

認識裂區實驗設計（split-plot design）：

　　以多層陶瓷電容器（Multilayer Ceramic Capacitors）為例，欲探討燒結爐溫度變化（1300°C、1400°C、1500°C）與內部電極不同印刷方法（P1、P2、P3、P4）對電容值的影響程度，因為改變燒結爐溫度設定並達到爐內溫度均衡相當不容易，因此溫度水準變化先採取逐漸升溫，再逐漸降溫的方式安排，無法採取完全隨機的方式進行溫度設定，而當每一次爐溫達到設定之實驗溫度時，則將不同印刷方式的陶瓷電容器同時隨機放置於燒結爐內不同的位置，實驗配置與執行情形，如表一。

　　此類型因為隨機限制所導致的實驗配置稱為裂區設計。因此，裂區實驗設計事實上包含兩種實驗單位（experimental units），也就是全區（whole plot）與副區（sub plot），從表一得知，六次重新設定（reset）不同溫度的燒結爐稱為全區實驗單位，而爐內四個不同的位置則稱為副區實驗單位。燒結爐溫度因為不易變更設定，所以無法與不同的印刷方式做完全隨機的實驗配置，而有隨機上的限制，因此安排為全區因子（whole-plot factors）；而不同的印刷方式則可以輕易的，完全隨機的放置於燒結爐內不同的位置，所以安排為副區因子（sub-plot factors）。

　　乍看之下，表一的實驗配置情形似乎與“完全隨機實驗”沒有兩樣，但注意如果按照“完全隨機實驗”的原則，每一種燒結爐溫度必須針對每一種印刷方式重新設定（reset）調溫，如此相同的實驗規模，則必須進行24次燒結爐的溫度重新設定。然而，若是按照裂區實驗設計，僅須進行6次燒結爐的溫度重新設定，每一次爐溫達到設定之實驗溫度時，再同時將四種印刷方式的陶瓷電容器一起隨機放置於爐內不同的位置。但也因為實驗配置與進行的方式不同，“裂區實驗”與“完全隨機實驗”的變異數分析方式也就不同。

分析裂區實驗設計：

　　從燒結爐加熱技術而言，因為燒結爐溫度重新設定所產生的實驗誤差（全區實驗誤差）將遠大於爐內不同位置所產生的實驗誤差（副區實驗誤差），所以必須分別推估兩種實驗單位所對應產生的實驗誤差，才能正確檢定出全區因子、副區因子或是兩者之間的交互作用是否有顯著的實驗效應。

　　因此，必須先將習慣的“完全隨機實驗”的變異數分析分解成全區與副區兩部份，分別探討其不同的變異來源（sources of variation）並計算其變異。全區部份的變異數分析，如表二，包含溫度水準重新設定所產生的變異來源與重覆三種不同溫度設定所產生的全區實驗誤差（whole-plot error）。

　　副區部份的變異數分析，如表三，則包含四種不同印刷方法所產生的變異來源，溫度與印刷方法之交互作用所產生的變異來源，和四種不同印刷方法在重覆三種不同溫度設定下所產生的副區實驗誤差（sub-plot error）。 

　　全區部份的變異數分析，因為燒結爐溫度重新設定所產生的全區實驗誤差偏大，自由度也偏低，因此造成統計檢定力（power of a statistical test）相對偏低。但本實驗之主要目的在比較不同的印刷方法對電容值是否有顯著影響，以及印刷方法與溫度之間是否存在顯著的交互作用，所以副區部份的變異數分析因為副區實驗誤差相對小，且有相對適當的自由度，已經擁有足夠的統計檢定力來檢出不同的印刷方法和印刷與溫度之間交互作用的顯著實驗效應。

　　本例之裂區實驗設計變異數分析中的平方和（Sum of Squares）、自由度（degree of freedom）與均方（Mean Square）的計算方法與一般“完全隨機實驗”完全相同，但是要特別注意，因為有兩個不同的實驗誤差來源，也就是全區實驗誤差和副區實驗誤差，所以必須將變異數分析分解成全區與副區兩部份。如果未注意此現象，而採取完全隨機實驗的方式，進行單一實驗誤差的變異數分析，將造成不正確的分析結果，如表四。

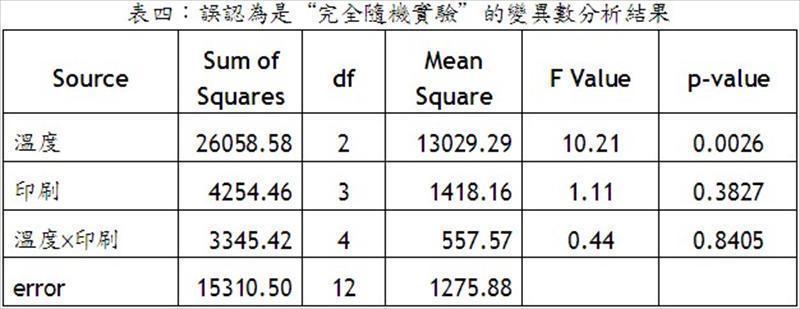
結語

　　在工業實驗的領域中，難免會遇到不易變化實驗水準的因子，此時裂區實驗設計就是可以考慮的另一種選擇，因此認知“裂區實驗設計”與“完全隨機實驗”在隨機限制上的差異和變異數分析過程的不同，對實驗者是有其必要性。

　　從實驗成本的角度，每變更一次實驗因子的水準必然多產生一筆實驗成本，以本例而言，燒結爐溫度（全區因子）僅須重新設定溫度6次，不必像“完全隨機實驗”必須進行24次的溫度重新設定，因此進行“裂區實驗設計”會比相同規模的“完全隨機實驗”節省許多實驗成本。

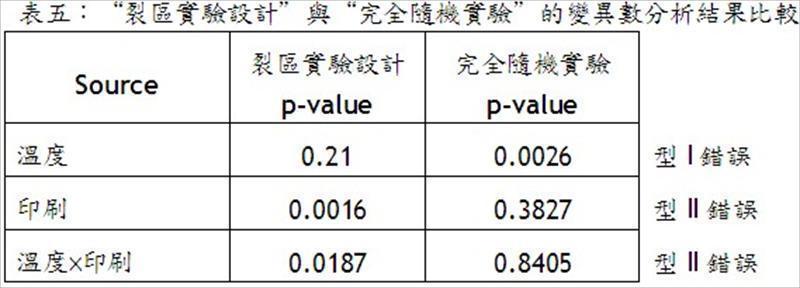
　　但裂區實驗設計會產生“全區”和“副區”兩種實驗誤差，若誤以完全隨機實驗的方式進行變異數分析，對全區因子而言，將造成型I錯誤（type I error）的增加，對副區因子而言，將造成型II錯誤（type II error）的增加，如表五。所以要切記將變異數分析區分成“全區”和“副區”兩大部分，才能同時確保裂區實驗設計的實驗成本優勢與準確的統計檢定結果。

參考文獻

1. Box. G.; Hunter. W.; and Hunter. S.﹙2005﹚. Statistics for Experimenters: Design, Innovation, and Discovery, 2nd edition. New York, NY: Wiley-Inerscience.