利用簡單比較實驗探討顯著性檢定

- 撰文者:
- 2013/02/21 瀏覽數:14654
前言:
當產品、流程或系統須進行改善時,負責人員常須判斷改善前後數據的不同,是由改變的效應所造成,或只是單純來自實驗誤差(experimental error)的結果,其實並無顯著差異。
以多層陶瓷電容器﹙Multilayer Ceramic Capacitors﹚為例,內部電極厚度﹙inner electrode thickness﹚是網版印刷﹙screen printing﹚製程中相當重要的的品質特性,在“相同”的製程條件設定與生產環境下,不同生產批次所量測的內部電極厚度數據自然就有不同程度的差異。因此當製程工程師須比較供應商所提供的新型網版與現行網版對內部電極厚度是否有不同的效果,進而安排並進行實驗後,緊接著就要面臨如何分析實驗數據,才能合理推斷兩種網版在印刷製程中對內部電極厚度所造成的效果有顯著差異,或是實驗觀察的結果只是來自實驗誤差的決策問題。
此時,顯著性檢定(significance testing),又稱為假設檢定(hypothesis testing),就在協助我們針對類似上述的效果比較問題,選擇適當的檢定統計量及運用對應的抽樣分配,在可容忍的錯誤機率前提下,判斷實驗因子水準(如新型網版與現行網版)改變後的結果,是否存在值得我們注意的顯著性差異。
實驗誤差:
在正式介紹顯著性檢定的程序之前,先說明實驗中產生誤差的必然性。
當實驗在盡可能相同的條件下重複進行,其實驗結果的數據不會完全相同,這種在重複實驗情形下所產生的波動稱為實驗誤差。實驗誤差是由系統的機遇變異原因(chance cause)所造成,是無法避免的,比如:量測儀器和實驗設備有限的精度、環境溫度與濕度的細微變化、材料本身的純度問題、以及操作人員的技術等都可能是造成實驗誤差的因素。
因此實驗者必須認知實驗誤差的存在,對實驗誤差與相對應的機率理論,﹙根據中央極限定理,實驗誤差會近似常態分配﹚,要有基本的瞭解,才能建立將來學習實驗設計與分析所必備的紮實基礎。但在這裡要特別注意實驗“誤差”不同於實驗“錯誤”,比如:實驗條件設定錯誤、看錯或記錯量測數據、操作程序或量測程序錯誤、用錯材料等。
統計量﹙statistic﹚與抽樣分配﹙sampling distribution﹚:
因為實驗誤差的存在,實驗的反應變數(response variable),如內部電極厚度,是一個隨機變數(random variable),其機率結構可用機率分配(probability distribution)來表示。實務上,隨機變數機率分配的平均值﹙μ﹚或變異數﹙σ2﹚等母體參數(population parameter)的真值是未知的,必須利用隨機樣本觀測值,透過樣本平均值﹙.jpg) ﹚或樣本變異數﹙s2﹚的公式,計算得到樣本平均值或樣本變異數來推估平均值或變異數等母體參數的真值。
﹚或樣本變異數﹙s2﹚的公式,計算得到樣本平均值或樣本變異數來推估平均值或變異數等母體參數的真值。
.jpg)
統計量定義為隨機樣本觀測值的函數,用來推論未知母體參數,因此,.jpg) 和s2均是統計量。而統計量的機率分配稱為抽樣分配,常態分配、t分配、卡方分配、F分配等都是常見的抽樣分配。(只要知道隨機樣本是來自何種類型的母體分配,通常就能夠決定統計量是屬於哪一種類型的抽樣分配,細節可參閱相關的統計推論書籍﹙1﹚。)
和s2均是統計量。而統計量的機率分配稱為抽樣分配,常態分配、t分配、卡方分配、F分配等都是常見的抽樣分配。(只要知道隨機樣本是來自何種類型的母體分配,通常就能夠決定統計量是屬於哪一種類型的抽樣分配,細節可參閱相關的統計推論書籍﹙1﹚。)
新型與現行印刷網版的簡單比較實驗:
在不影響多層陶瓷電容器相關電性與內部電極連續性的前提下,製程工程師希望其內部電極厚度可以愈薄愈好,如此便可以減少內電極膏的單位使用量,進而降低產品單位成本。因此當供應商提供聲稱可以有效降低內部電極厚度的新型網版時,製程工程師便針對現行網版與新型網版安排並進行完全隨機實驗﹙completely randomized design﹚,分別蒐集10批內部電極厚度數據,如表1。
.jpg)
表1:新型網版與現行網版內部電極厚度的實驗數據﹙um﹚
這種單純比較兩種條件﹙新型網版與現行網版﹚的實驗,通常稱為簡單比較實驗。
分別計算兩種不同種類網版其內部電極厚度樣本平均值︰
新型網版內部電極厚度樣本平均值
.jpg)
現行網版內部電極厚度樣本平均值
.jpg)
因為在正常的生產過程中,批與批之間的數據本身就有不同程度的差異,即使兩種網版內部電極厚度平均值之間有差異,但是否大到足以顯示兩種網版所造成的效果確實有差異,或是實驗觀察的差異只是來自實驗誤差,也許兩種網版其實效果相同。顯著性檢定便是可以幫助工程師回答此問題的一種統計推論方法。
顯著性檢定(significance testing):
西元1933年,由波蘭人奈曼(Jerzy Neyman, 1894-1981),及英國人皮爾生(Egon Pearson, 1895-1980),提出著名的奈曼-皮爾生引理(Neyman - Pearson lemma), 奠定了一套假設檢定的架構。
基本上顯著性檢定可以按照以下的步驟進行
1. 陳述虛無假設與對立假設
2. 選擇顯著水準
3. 隨機抽取樣本
4. 計算檢定統計量與相對應的p值
5. 決定“拒絕”或“接受” 虛無假設
現在就簡要的介紹每一個步驟
陳述虛無假設與對立假設︰
以本文個案為例,雖然供應商宣稱在相同的製程條件下,使用新型網版可以降低內部電極厚度,但我們先假設兩種網版對內部電極厚度的效果沒有差異,再蒐集隨機樣本,從隨機樣本中判斷是否有“不尋常的證據”足以“拒絕”原先的假設,否則便“接受”原先的假設。
現在把它轉換成統計假設問題,首先須陳述虛無假設(null hypothesis),以Ho表示,通常虛無假設表示無差異,而對立假設(alternative hypothesis)則表示有差異,以Ha表示。正式的陳述方式如下:
.jpg)
雖然我們想證明Ha是真的,然而除非證據夠強,否則不輕易“拒絕”虛無假設,因為“拒絕”虛無假設時,通常就代表要改變現狀,也就是要採用新型網版取代現行網版,當然在作決策前須考慮得更周全。因此要從樣本中判斷是否有“不尋常的證據”足以“拒絕”原先的假設,只是尋常與不尋常要如何區隔呢?而其中的關鍵就在於機率。
選擇顯著水準:
顯著水準﹙α﹚就是以機率值來表達,用來量化需要多麼“不尋常的證據”,才能拒絕虛無假設,也就是當隨機抽樣樣本出現的機率值小於α時,便可以拒絕虛無假設,常用的顯著水準有0.1,0.05,及0.01等,顯著水準愈小,代表需要愈“不尋常的證據”,才能否定虛無假設。
在本案例中,製程工程師指定顯著水準α=0.01,表示隨機抽樣樣本出現的機率值小於0.01的事件,可以被視為是機率理論中的小機率事件,也就是長期而言,這樣的事件應該在100次試驗中平均最多出現一次,因為出現的機率相當低,代表實際上不太可能會發生,而如果在一次的隨機抽樣中就出現了,便是“不尋常的證據”,因此懷疑原先假設的合理性,進而“拒絕”虛無假設。
隨機抽取樣本
顯著性檢定假設實驗觀測值是獨立隨機變數﹙independent random variables﹚,只要以隨機方式安排實驗進行順序,通常就可以滿足此一假設。本文案例的實驗順序便是以隨機方式安排進行,如表2。
.jpg)
表2:以隨機方式安排實驗進行順序
計算檢定統計量與相對應的p值:
如圖1所示的盒鬚圖﹙box-and-whisker plot﹚,可以讓實驗者輕易快速的看出兩種網版的內部電極厚度數據的變異程度大致上是相同的。(兩母體的變異數是否有顯著性差異,可以利用F統計量進行檢定,細節可參閱相關的統計推論書籍﹙1﹚。)
.jpg)
圖1:新型網版與現行網版內部電極厚度的盒鬚圖
如果新型網版與現行網版內部電極厚度的變異數無顯著性差異,便可以利用to統計量來比較兩母體平均數。
.jpg)
其中 和
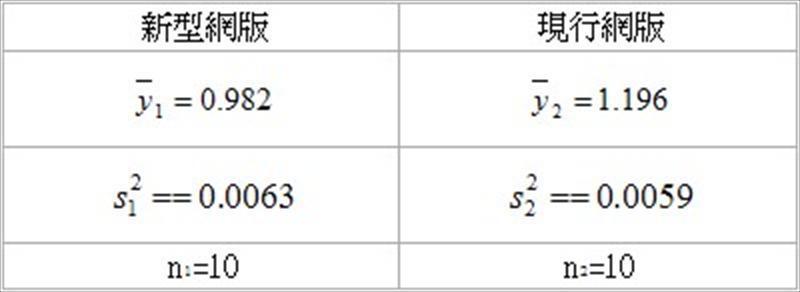
和.jpg) 是樣本平均值,n1和n2是樣本數, 是共同變異數(common variance)
是樣本平均值,n1和n2是樣本數, 是共同變異數(common variance)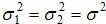 的估計量,其公式為
的估計量,其公式為
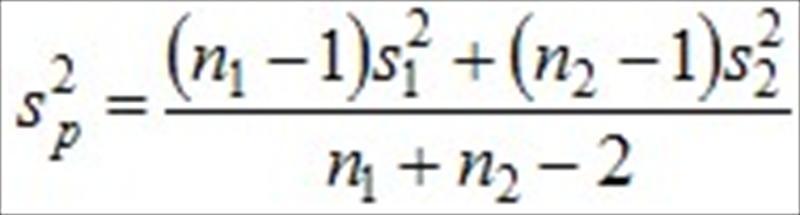
其中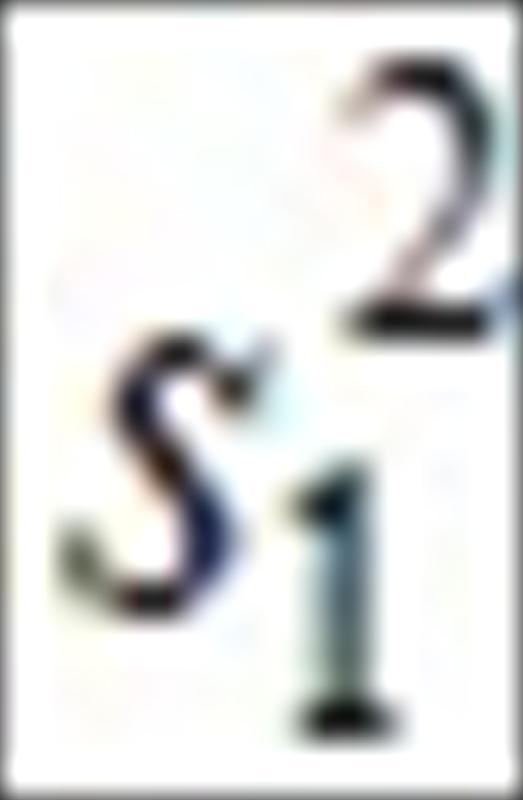 和
和.jpg) 是樣本變異數,利用表1的實驗數據,可以得到檢定統計量
是樣本變異數,利用表1的實驗數據,可以得到檢定統計量
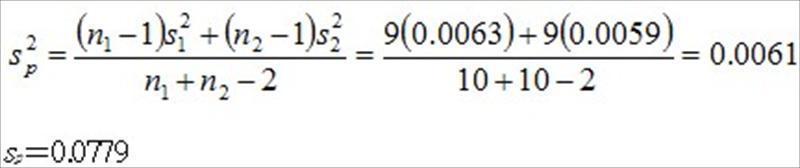
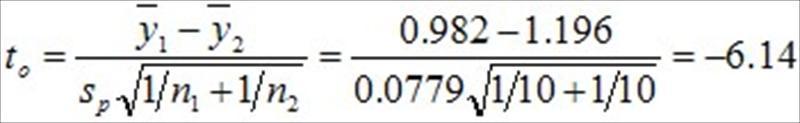
如果Ho為真時,則to檢定統計量的抽樣分配就是符合自由度為n1+n2-2的t分配,也就是利用t分配,可以描述to檢定統計量的機率規律行為。
因為to=-6.14,自由度為18,運用EXCEL軟體內建的t分配統計函數,TDIST(x,degrees_freedom,tails),{ 其中x=to=-6.14,degrees_freedom=自由度=18,tails=1表示回傳單尾分配,tails=2表示回傳雙尾分配,本例為雙尾檢定,因此選擇tails = 2 },依序輸入函數內所需之數值後,可以輕易計算得到比出現to=-6.14更極端值的累積機率值,也就是p值=0.000008。{ 因為tails = 2,TDIST 以 TDIST = P(|X| > x) = P(X > x or X < -x) 來計算 }。
決定“拒絕”或“接受”虛無假設
在本案例中,指定顯著水準α=0.01,因為計算得到p值=0.000008小於α,根據上述小機率事件不應該在一次試驗中就出現的原理,也就是說,如果Ho為真時,不應該會出現這樣“不尋常”的實驗結果,因此懷疑原先假設的合理性,進而“拒絕”虛無假設,所以推論新型網版與現行網版內部電極厚度的平均值有顯著性差異。
{ 另一種情形,如果根據實驗結果計算得到p值大於α,則代表樣本未能提供顯著的證據,不能“拒絕”虛無假設,只好“接受”虛無假設 }。
兩種錯誤類型
依據實驗數據所推論顯著性檢定的結果,不論是接受或拒絕虛無假設都有可能會犯錯誤,以誤判的類型而言,事實上有兩種可能錯誤的機率,如表3,一種是當虛無假設為真時,應該接受它,卻拒絕它,稱為第一類型錯誤,另一種則是虛無假設不為真時,應該拒絕它,卻接受它,稱為第二類型錯誤。
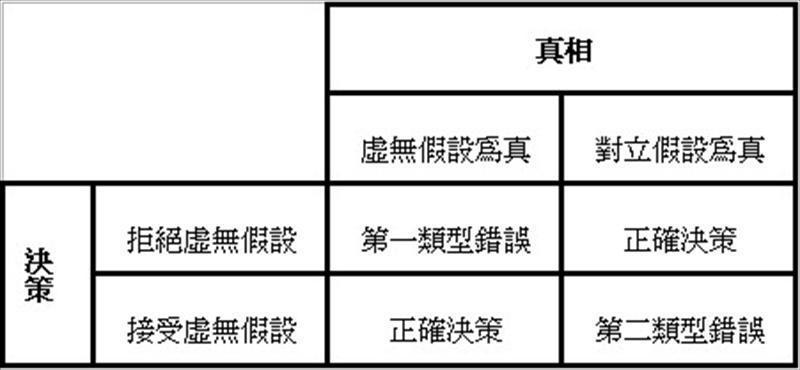
表3:第一類型錯誤與第二類型錯誤
第一類型錯誤,以希臘小寫字母α表示,就是前述檢定的顯著水準,因為在檢定的程序中可以事先指定,所以是我們可以直接控制的錯誤風險。當檢定計算所得的p值小於α值時,因為認定如果虛無假設為真時,不應該會出現這樣的抽樣結果,所以便決定“拒絕”虛無假設,但是當我們做這樣的決策時,必須理解雖然發生的機率相當低,仍然“有可能”會發生,因此有可能我們做了錯誤的決策,這就是所謂的第一類型錯誤。為儘量避免造成這種錯誤,因此要採取較保守的α值,也就是0.1,0.05,或0.01,當考量第一類型錯誤所衍生的負面後果可能愈嚴重時,就要指定愈小的α值。
第二類型錯誤,則是以希臘小寫字母β表示。而當虛無假設不為真時,可以正確的“拒絕”虛無假設的能力則稱為檢定力﹙power of test﹚,也就是1減去發生第二類型錯誤的機率,亦即檢定力=1-β,一般建議檢定力至少為0.8。在指定顯著水準﹙α﹚後,在相同的樣本數下,β值會直接受到檢定對象的效果差異量﹙effect size﹚的影響,效果差異量愈大,愈容易被發現其存在顯著差異,β值就愈低,檢定力也就愈高,﹙因為檢定力與β兩者機率值互補正好為100%﹚,如表4。

表4:雙尾t檢定,顯著水準﹙α﹚=0.01,樣本數n1=n2=10,在相同的樣本數下,效果差異量愈大,發生第二類型錯誤的機率愈低,檢定力也就愈高。
因此,為確保有足夠的檢定力可以發現檢定對象特定的效果差異量,就要先計算需要抽取的隨機樣本數大小,方能避免β值過高,如圖2。
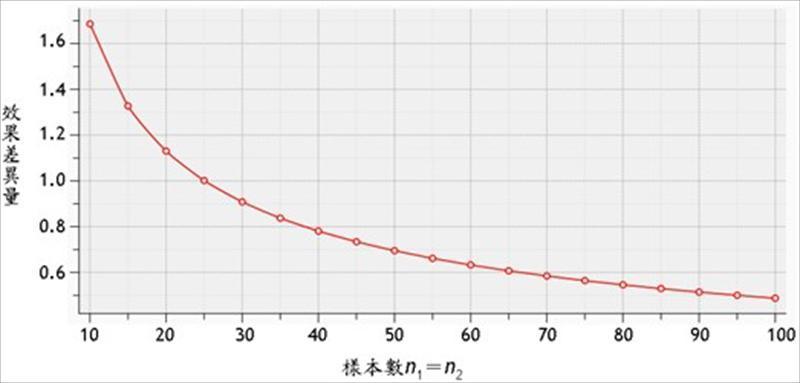
圖2︰雙尾t檢定,顯著水準﹙α﹚=0.01 ,為確保檢定力至少為0.8,預期偵測的效果差異量﹙﹙μ1-μ2﹚∕σ﹚與樣本數之關係。
結語:
在真實的隨機世界中所提出的統計假設是否為真,通常都無法百分百確定,只能在現實的條件中,儘可能的減少誤判的機率。雖然理想狀況是希望兩種錯誤機率皆為0,但通常不存在這種情形,所以進行假設檢定時,要事先考慮可以容忍的推論錯誤機率,以做為判定“拒絕”或“接受”虛無假設的準則。
而顯著性檢定是以保護虛無假設為原則,因此欲“拒絕”虛無假設,必須掌握“不尋常的證據”,也就是不應該在一次試驗中就出現的小機率事件,i.e. p值<顯著水準α,發生的機率要夠小才能稱為顯著,除非有顯著的差異,否則寧可維持現狀。
當“拒絕”虛無假設,認定有顯著性差異時,還要分辨統計顯著性﹙statistical significance﹚與實務顯著性﹙practical significance﹚之間的區別。如果觀測的的差異效果,大到某種程度,單純靠機遇或實驗誤差產生這種結果的機率很小,也就是差異效果的發生並非偶然時,就稱此差異效果有統計顯著性。而實務顯著性則是指差異效果在真實的世界中是可以產生實際效用。
因為只要樣本數足夠大,即使是沒有實務效益的微小差異也會造成統計顯著性。因此當檢定結果有統計顯著性差異時,還要特別注意其差異在真實的世界中是否有實質意義,也就是要可以反映技術或應用上的具體改善效益等。
參考文獻:
1. Montgomery, D. C. ,and Runger, G.C. ﹙2003﹚. Applied statistics and probability for engineers,Wily, New York.
防火管理人訓練初訓班(桃園班)
上課時間 2026/07/23 ~ 2026/07/24
國際貿易與保稅區廠商之稅賦規劃解析
上課時間 2026/05/14 ~ 2026/05/14
荷重在一公噸以上之堆高機操作人員安全衛生教育訓練班(夜間班) - (不含檢定費1820元夜間班 - 課程費用優惠中 - 上課學員送檢定報名表
上課時間 2026/11/10 ~ 2026/11/15
公共工程品質管理人員回訓班 - 路面工程品質管理實務(一)(二)_假日實體班 - (六日整天) - 紙本4/30前寄達 - 請勿繳費待上課通知
上課時間 2026/05/16 ~ 2026/05/31
出納作業、資金流量分析及有效調度實務班 - LINE@ID:@274aywrg - 許文西老師
上課時間 2026/05/05 ~ 2026/05/05
ISO14064-1:2018 組織溫室氣體內部查證員訓練 - (實體+遠距同步) - 第二梯 - 可自備筆電
上課時間 2026/04/29 ~ 2026/04/30
急救人員安全衛生在職教育訓練班 - (上午班) - 請上傳結業證書 - (當天發證明)
上課時間 2026/07/03 ~ 2026/07/03
商業談判術(B2B)
上課時間 2026/12/17 ~ 2026/12/17
PLC控制器入門實作班(數據與結構化設計)
上課時間 2026/12/11 ~ 2026/12/23
固定資產管理與盤點實務
上課時間 2026/06/12 ~ 2026/06/12












