運用客戶實際生產量解決預估失準之實務應用

　　企業營運根據上、下游關係，同時擁有客戶與供應商兩種的角色［如圖一］，企業內部也會存在這兩種關係的單位，譬如組裝廠（內部客戶）與射出成型廠（內部供應商）或組裝廠（內部客戶）與包材廠（內部供應商）等［如圖二］，內部供應商必須滿足內部客戶的需求自是理所當然，然而，若組織運作不適當，往往會造成「內部供應商」的困擾。以下案例是某公司實際發生的情況。

［圖一］

［圖二］

　　T企業是一家集團公司，有多個分公司與事業部［如圖三］，其中有一公司事業部，D事業部，所生產的產品並不對外銷售，而是提供材料給各事業單位，形成所謂的內部供應商。D事業部雖然是內部供應商，同樣的，也須背負營運上的品質、成本、交期等等的管理。

［圖三］

　　由於D事業部的角色特殊，必須滿足內部客戶的生產需求，儘管各事業部都會共同參與月產銷會議，也會提供週排程計畫，但總有「計畫趕不上變化」的無奈感，長期以往，插單、改單的情形演變成家常便飯，庫存數也難以有效控制，成了D事業部資材單位的痛點。

　　幸好，T企業不僅有完善的企業資源規畫系統（Enterprise Rresource Planning，ERP），也有自行開發的製造執行系統（Manufacturing Execution System, MES），兩系統皆蒐集了龐大的數據，若能有效的利用這些數據，來預測各事業部的月產銷計畫量，並檢視預測與事業部生管給的預估量之差異是否過大，從而提出問題，重新審視預估量。

　　我們挑選A、B、C一事業部來做預測。首先，我們從MES系統下載2016年1月到2017年12月某事業部的生產數據，如［圖四］。

［圖四］

　　從上圖可知，2016年1月至2017年12月之間，該事業部的產量有逐月上升的趨勢，但在2016年2月與2017年1月卻突然往下降，原因是當月正好是農曆過年，工作日數較其它月份少，產量自然也較少。

　　然而，預測方式有很多類型，究竟要選擇哪一類型的預測方式？由於是下載一段時間內的資料，因此，我們採用「時間序列」的方式來做預測，故我們使用不同「時間序列」的預測模型來預估。

　　移動平均法（Moving Average Method, MA）是定量需求預測方法中較簡單的一種，它是利用過去數期的需求資料來建立預測值，其移動平均值是以特定的期數，如3個月、4個月或5個月等來計算，數學式如下

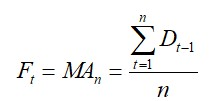
　　其中，Ft=第t期的預測值，Dt-1=第t-1期的需求量（實際值），n=移動平均的期數。

　　對於本文所提出的數學式，實務上，我們不太可能用筆計算並比較。因此，我們利用EXCEL試算表來實現計算過程與結果，配合EXCEL試算表公式的呈現有助於理解數學式所代表的意義。故我們以EXCEL試算表計算上述數學式的預測值，如［表一］。

［表一］

　　我們舉「2期預測」與「3期預測」說明EXCEL試算表的公式設定，餘期，依此類推，如［表二］。

［表二］

　　用了這麼多的期數來預測，到底哪一期的預測方式比較好？我們可以用實際值與預測值之間的差距來定義「預測誤差」（error），計算式如下：

　　其中，et=第t期的預測誤差，Dt=第t期的需求量（實際值），Ft=第t期的預測值

　　RSFE表示累計誤差（Running Sum of Forecast Error）

　　然而，僅是以這樣的計算方式衡量預測誤差，在正、負誤差的影響下，會導致RSFE值的失準，因此，我們決定使用其它的方法來判斷預測準確度。

　　MAE表示平均絕對誤差（Mean Absolute Error），其中n代表期數

 　　RMSE表示均方根誤差（Root Mean Square Error）

　　MAPE表示平均絕對百分比誤差（Mean Absolute Percent Error）

　　這三項評估指標的結果，數值愈小代表誤差愈小，預測的結果愈準確。由於MAE與RMSE計算誤差皆會有計算誤差值大小取決於預測項目衡量值大小的問題，在某些情況下，預測值與實際值的誤差比例遠比預測誤差的絕對數字更具參考價值，MAPE不僅僅考慮預測值與實際值的誤差，還考慮了誤差與實際值之間的比例。

　　學者Lewis（1982）認為，MAPE是最有效的評估指標，並將MAPE分為四種等級，如［表三］所示。

［表三］

　　因此，本篇案例將選用平均絕對百分比誤差（MAPE）為主要的指標來衡量誤差，以判斷預測值的準確程度，同時輔以平均絕對誤差（MAE）及均方根誤差（RMSE）做為比較誤差之準則，利用這些指標，找出較佳的預測模式。

　　我們選「2期預測」作為範例，以EXCEL試算表分別計算MAPE、RMSE與MAE值，如［表四］。

［表四］

　　同時說明EXCEL試算表的公式設定，餘期，依此類推，如［表五］。

［表五］

　　依照［表四］的方式，我們計算出各期MAPE、RMSE與MAE的誤差值並彙整如下，如［表六］。從［表六］可以得知，在這個案例中，移動平均法的期數愈多，MAPE的誤差愈大，以4個月期的MAPE，18.16%，誤差最小，若以學者Lewis 區分的等級來說，屬於優良的預測。

　　然而，這樣就可以結束了嗎？不，前面提到，2016年2月與2017年1月的產量突然往下降的原因是碰上農曆過年，因此，我們把這兩個月的資料另外處理，再重新計算各期的MAPE、RMSE與MAE，看看會發生什麼情況，如［表七］。

［表六］

［表七］

　　我們發現，這樣處理後，各期的MAPE、RMSE與MAE值明顯變小了，4個月期的MAPE依然是誤差最小，10.22%，可見得這兩個月的數據足以影響整個預測模型的結果，因此，後續的預測模型將不包含這兩個月的資料。繪製誤差最小MAPE之4期預測值與實際量，如［圖五］所示。

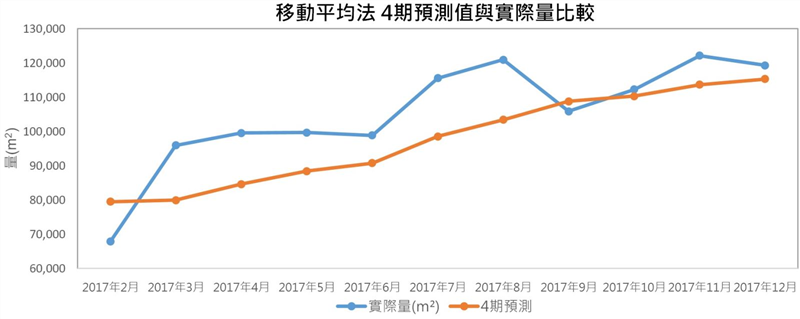
［圖五］

　　移動平均法的優點在於容易計算與了解，缺點是每一期權重都相同，若在序列中有變動發生，則移動平均預期的反應會很遲緩。若我們想藉由調整移動平均法使其更準確的反映資料中的波動情況，則可給予近期資料較高的權重，此種方法稱為加權移動平均法（Weighted Moving Average, WMA），其數學式如下：

　　其中，F_t=第t期的預測值，W_t-1=第t-1期的權重值，D_t-1=第t-1期的需求量（實際值），n=移動平均的期數。

　　權重的選擇，最常用的方式是經驗法和試誤法，但是我們可以設定不同組的權重，然後透過試預測進行比較分析，選擇預測誤差小者作為最終的權重。我們以5個月期及其一組權重值作為範例，以EXCEL試算表計算預測值，如［表八］。

［表八］

　　同時說明EXCEL試算表的公式設定，餘期，依此類推，如［表九］。

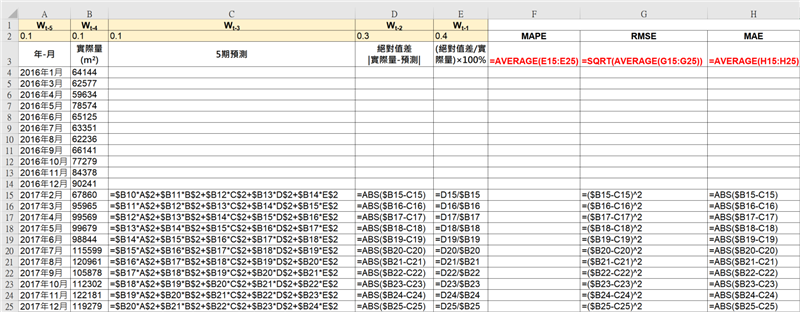
［表九］

　　最後，我們將各期數與不同權重的預測誤差彙整為一張表，如［表十］。

［表十］

　　從［表十］的MAPE值可以得知，當計算週期為3個月期，權重值為0.2、0.2及0.6的加權移動平均法，可以有最低的MAPE值，故預測2017年2月到2017年12月的生產量時，以此為準。繪製3期（W_i=0.2、0.2與0.6）預測值與實際量，如［圖六］所示。

［圖六］

　　當移動平均間隔中出現趨勢時，給近期實際值賦予較大的權重，給遠期實際值賦予較小的權重，進行加權移動平均，預測效果較好。但要為各時期分配權重並找出合適的權重值是一件非常耗時的事。為能經濟有效的處理，並提供良好的短期預測，「指數平滑法」是不錯的選擇，其數學式如下：

　　其中，F_t=第t期的預測值，F_t-1=第t-1期預測值，D_t-1=第t-1期的需求量（實際值），α為平滑係數（0<α<1）。α→0，表示預測誤差的調節能力小（平滑度高，愈相信預測值）；α→1，表示預測誤差的調節能力大（敏感度高，愈相信實際值）

　　在計算的過程中我們會發現，上式需要有期初預測值，一般可以選取上一期的實際值、移動平均法求得或前幾期觀測值的平均值作為初始值。

　　我們以α=0.6作為範例，初始值設為預測期之前三期的平均值，以EXCEL試算表計算預測值，如［表十一］。

［表十一］

　　同時說明EXCEL試算表的公式設定，餘期，依此類推，如［表十二］。

［表十二］

　　最後，我們將不同α值的預測誤差彙整為一張表，如［表十三］。

［表十三］

　　從［表十三］得知，當指數平滑法的α值設為0.7時，可以使2017年2月到2017年12月的預測與實際量有較好的MAPE值10.24%，再進一步分析發現，α值設為0.71時，有最低的MAPE值10.22%。而其預測值與實際量的比較，如［圖七］所示。

［圖七］

　　上述的指數平滑法適合用在數據比較平穩，沒有較大的波動時，也稱為一次指數平滑法，如果數據具有某種趨勢，但無季節變動，則二次指數平滑法是較為實用的方法。從［圖四］可以知道，該事業部的生產量有逐月上升的趨勢且無季節變動，因此，我們採用 Robert G. Brown 單一參數線性指數平滑法來解決這一問題，其數學式如下：

　　式中，T為預測的期數

　　又

　　且

　　式中，為一次指數平滑值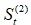，為二次指數平滑值，D_t=第t期的需求量（實際值），α是平滑係數（0<α<1）。

　　當t=1時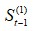， 與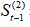都是沒有數據的，需事先給定，通常採用 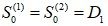或序列最初幾期數據的平均值。在這個案例中，我們以α=0.3作為範例，初始值我們採用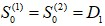，以EXCEL試算表計算預測值，如［表十四］。

［表十四］

　　同時說明EXCEL試算表的公式設定，餘期，依此類推，如［表十五］

［表十五］

　　最後，我們將不同α值的預測誤差彙整為一張表，如［表十六］。

［表十六］

　　從［表十六］得知，當二次指數平滑法的α值設為0.2時，可以使2017年2月到2017年12月的預測與實際量有較好的MAPE值9.35%，再進一步分析發現，α值設為0.21時，有最低的MAPE值9.27%，以學者Lewis 區分的等級來說，屬於高精準的預測（MAPE<10%）。而其預測值與實際量的比較，如［圖八］所示。

［圖八］

　　迴歸分析（Regression analysis）除了可以用來觀察兩個或兩個以上的變數之間的因果關係外，還可以被用來作為時間序列的預測工具。我們以時間（t）為自變數，生產量（y_t）為應變數，隨著時間的變動來預測生產的需求量，由於該事業部的生產量有逐月上升的趨勢，如［圖四］，因此，我們可利用最小平方法（Method of least squares）求得線性迴歸模型（Linear regression model）：

　　其中，

　　式中，y_i=第t期的預測值，a:在t=0時的y_i值，b表示直線斜率，n為期數。

　　我們以EXCEL試算表先用2016年的資料（不含2月份）求得初始的迴歸方程式，如［圖九］，再用此迴歸方程式求得次月（即2017年2月）的需求預測，如［表十七］。

［註:迴歸方程式 x以t替代；EXCEL試算表可以設定顯示公式］
［圖九］

［表十七］

　　將2017年2月份的實際量填入後，求得絕對值差、（絕對值差/實際量）×100%。再利用2016年 （不含2月份）到2017年2月份，12筆實際生產量的數據以迴歸分析法預測2017年3月的生產量，如［表十八］。

［表十八］

　　依此方式，由EXCEL試算表完成至2017年12月份的資料，如［表十九］。

［表十九］

　　最後，我們計算2017年2月到2017年12月的MAPE、RMSE、MAE值分別為9.10%、10571.8及8970.2，其預測值與實際量的比較，如［圖十］所示。

［圖十］

　　本案例使用了移動平均法、加權移動平均法、指數平滑法與線性迴歸模型四種預測方法之52種模型來預測未來需求量，其預測模型整理如下：

1. 移動平均法

以特定期數2個月期、3個月期、4個月期、5個月期、6個月期、12個月期，共6種模型。

2. 加權移動平均法

以2個月期加權權數4種組合、3期加權權數8種組合、4期加權權數7種組合、5期加權權數6種組合，共25種模型。

3. 指數平滑法

一次指數平滑法，平滑指數α值0.1至0.9，共10種模型。

二次指數平滑法，平滑指數α值0.1至0.9，共10種模型。

4. 線性迴歸模型

線性迴歸預測方式1種模型。

分別將四種預測方法較佳的模型與條件整理如下，如［表二十］：

［表二十］

　　因此，本案例採用線性迴歸模型做為次月的預測模型，同時，比較生管排程的計畫量與預測量，結果發現以預測的方法比生管計畫有較少的誤差，如［表二十一］，此預測方法已導入該事業部，可以有效減少生管插單、改單與庫存的情形。

［表二十一］

　　前文提到，過年當月的工作天數遠遠少於其它月份，著實影響整個預測模型，因此必須另外處理，處理的方式可以使用其它方法建立模型，但由於本案例的過年月份數據少，不足以建立模型，因此暫時予以忽略。

　　本文雖然使用內部客戶生產量來預測，亦可使用自己出給內部客戶的出貨量來預測，實務上，我們對於外部顧客的生產量是無法得知，但可以運用本身出給該客戶的數量來預測。

總結

　　預測方法的種類非常多，究竟要選用哪一種方式？最佳的預測方法也不一定是準確度最高或是成本最低，而是取決於管理者對預測的準確度與成本的需求。

　　就本例而言，四種預測方法都比生管計畫要來得準確許多，最後採取迴歸分析法來預測次月，因為它的模型誤差最小，但不代表每個月都是以迴歸模型來預測，而是以這四種模型中哪一個月的預測誤差最小，當作是次月的預測模型，一旦預測誤差愈來愈大時，參考［表三］，代表預測模型已不適用，必須另覓他法。

　　預測分析的目的在於後續的管理策略為何？本文的案例，主要是要解決內部客戶預估失準所造成的庫存增加；因庫存問題可能造成的品質隱患；插單、改單與追加訂單造成的成本增加，如加班、人力調度、物料需求調整等等。根據預測數據，生管可以評估後續的管理策略，以提供上一階主管做管理決策。如［圖十一］所示。

［圖十一］

　　除此之外，生管可以依據預測數據來檢視內部客戶提供的預估是否超過預測自設的比例，一旦超出，便須更進一步地向內部客戶確認預估的可靠性，從而減少計畫排程的變異，進而減少不必要的成本與浪費，解決這些問題該事業部生管導入預測的主要目的。

　　儘管預測模型的選用是重要的事，更重要的是，就算模型預測得非常準確，若沒有採取任何的管理策略，「預測」這件事情也就沒有多大的意義。

【參考資料】

1. 陳寬茂（2004）。CPFR流程下之訂單預測方法。國立政治大學資訊管理研究所碩士論文。
2. 楊明德（2012）。銷售預測之研究-以T公司花蓮營業處為例。國立東華大學管理學院高階經營管理碩士在職專班論文。
3. 指數平滑法。
4. 百度。指數平滑法中平滑系數的選擇研究。